Dalam tutorial ini saya akan memberikan contoh bagaimana untuk menciptakan sebuah poster teaser film seperti gambar yang di samping!!!

Langkah 1 : Mulailah dengan sebuah kertas baru warna hitam gelap # 080808 dengan W=1600  pixel dan H=2300 pixel dengan resolusi=300 pixel/inch.

Langkah 2 : Tambahkan latar belakang agar lebih menarik. Di sini saya menggunakan gambar tekstur kertas bernoda(bisa cari di internet).Kemudian pilih image-adjustment-pilih desaturate lalu atur blending mode dan pilih "hard ligth" lalu tarik opacity ke 30%.

Langkah 3 : Tambahkan gambar Nebula (bisa cari di internet) di dalam lapisan baru di atas tekstur, dan pilih Hue/Saturation (192, 26, 0). Ini harus memberikan warna biru (lihat gambar di bawah). Sekarang gunakan "add layer mask" untuk menggabungkan gambar nebula tadi dengan latar belakang. Hanya kiri, kanan dan bawah yg harus di "add layer mask" (lihat gambar dibawah).

Langkah 4 : Selanjutnya adalah menambahkan gambar cakrawala(bisa cari lagi diinternet). Sama seperti langkah-langkah sebelumnya, "desaturate" gambar dan pilih "soft light" pada pilihan mode blendingnya. kemudian gandakan gambar agar dapat ditampilkan sedikit lebih rinci. Lalu gunakan "gradient tool "untuk menutupi gambar dari atas. Karna kita hanya perlu melihat gunung /batuan dan sepotong kecil dari langit(lihat contoh gambar di bawah).

Langkah 5 : Cari gambar sosok wanita /pria sesuai pilihan anda(setengah badan). Disini saya memakai gambar wanita dan  kemudian meletakkannya di gambar nebula. Saya juga menggunakan kekuatan smudge tool 30%) untuk memberikan efek  di wajah dan lengan(lihat gambar dibawah).

 Langkah 6 : Gunakan "pen tool"Anda untuk menggambar bentuk pada pipi perempuan itu. Bentuk shape dan Warna yang digunakan ditunjukkan pada gambar.

Langkah 7 : Buat bentuk shape nampak lebih mengkilap lagi dengan menggunakan brush warna putih dengan opcitity  20 %.

Langkah 8 : Masukan suatu gambar perangkat chip komputer misalnya, lalu "add layer mask" dengan bentuk shape yg berwarna biru tadi hingga hasilnya seperti yg terlihat pada gambar dibawah.

Langkah 9 : Membuat layer baru dan menggambar dua bentuk shape berwarna kuning dengan "pen tool" seperti ditunjukkan pada gambar. Lalu lakukan hal yg sama seperti shape yg sebelumnya kita buat. Dan hasilnya seperti gambar berikut :

Langkah 10 : Untuk membuat karakter lebih "superhero" saya menambahkan cahaya ke matanya.Hanya menggunakan "brush tool" di atas mata (warna: # 10bdee) dan set opacity menjadi 50%, maka hasilnya seperti berikut :

Langkah 11 :Buat folder bernama "color adjustment" dan letakkan di bagian atas semua lapisan anda. Dengan cara itu akan mempengaruhi semua lapisan di bawahnya(lihat gambar di bawah).
Solid Color:
Color fill: # 020317

Selective color:
Merah: 37, -10, -33. +30
Kuning: +25, 0, -15, 0
Netral: +5, 0, +2, +2
Black: +20, 0, 0, 0

Brightness / contrast:
Brightness: 11
Contrast: 7

Langkah 12 : Pilih lapisan wanita. Gunakan "lasso tool" untuk membuat  garis di bagian leher agar membuat suatu efek potongan. Gunakan inner shadow pada blend optionnya dan anda mendapatkan hasil seperti yang ditunjukkan pada gambar dibawah . Untuk bagian lengan saya melakukannya sedikit berbeda. Saya membuat garis seperti gelang dan mengisinya dengan warna: # 705e53. Kemudian memberinya efek inner shadow pada option blendnya.

Langkah 13 : Untuk menambah animasi, pada shape di bagian lengan(lihat gambar dibawah) kita dapat menggunakan langkah-langkah  yg saya jelaskan sebelumnya.Di sini saya menambahkan simbol listrik.

Langkah 14 : Sisanya dari tutorial ini adalah benar-benar sampai imajinasi anda sendiri. Untuk bagian ini,saya menambahkan helicopter dan menggunakan pilihan "tool brush" efek petir(download di internet). Biarkan kreativitas anda berlari bebas dan silahkan menambahkan apapun yang anda inginkan.

Langkah 15 : Langkah terakhir tinggal menambahkan teks "SUPER HEROES". Saya menggunakan efek petir untuk menutupi teks, lalu kaburkan teks menggunakan "erase tool"  dengan opacity 30% di beberapa bagian(lihat gambar dibawah). Untuk menyelesaikan gambar dan membuatnya lebih tajam saya menggunakan "smart sharpen " (filter-sharpen). Set menjadi sekitar 50%. -------- SELESAI --------

Materi Invers Matriks
(download disini)

Materi Interpolasi
[download disini]

Materi Integral 

{download disini}

Persamaan linier :

1.    *  Persamaan yang semua variabelnya berpangkat 1

Contoh:  x  +   y  + 2z =  9

Solusi: berupa suatu “tripel” dengan masing-masing nilai sesuai urutan (nilai-x, nilai-y, nilai-z) yang memenuhi persamaan tersebut.

Himpunan solusi untuk persamaan di atas:

{ … ( 0, 1, 4), (1, 0, 4), (4, 5, 0), …. }

Himpunan solusi juga disebut Ruang Solusi (solution space)

2.       

     *Suatu sistem dengan beberapa (2 atau lebih) persamaan linier.

Contoh:  x  +   y  =  3

                3x  –  5y =  1

 Ruang Solusi: berupa semua ordered-pair (nilai-x, nilai-y) yang harus  memenuhi semua persamaan linier dalam sistem tersebut untuk sistem ini ruang solusinya { (2, 1) }

untuk lebih lengkapnya; Silahkan Download materinya <klik di sini>

Algoritma Metode Newton Raphson:

1. Definisikan fungsi f(x) dan f¹(x)
2. Tentukan toleransi error (e) dan iterasi maksimum (n)
3. Tentukan nilai pendekatan awal x₀
4. Hitung f(x₀) dan f^’(x₀)
5. Untuk iterasi I = 1 s/d n atau |f(x_i)|> e

R  Hitung f(x_i) dan f¹(x_i)

R  Akar persamaan adalah nilai x_i yang terakhir diperoleh.

1.      Program menghitung nilai x dari persamaan f(x) : x² + 3x – 10 dengan menggunakan metode Newton Rapshon.

Deksripsi :

            Metode Newton Rapshon menggunakan formula atau algoritma untuk mendapatkan nilai x maka :

*. x[n+1] = x[n] – f(x)/f`(x)

*.  Parameter awal x diinput dan nilai e = 0.0005

*.  f(x) = fungsi persamaan x² + 3x – 10 = 0, maka x = 2 atau x = -5, jadi kita menginputkan bilangan x awal apabila mendekati 2 maka hasil x akhir = 3, dan apabila mendekati = -5 maka hasil x akhir = 5

*.  f`(x) = fungsi turunan pertama f(x) 2x + 3

*.  nilai e = 0.0005

*.  kondisi dimana perulangan berhenti nilai mutlak (Absolute) |x[n+1] – x[n]| < e, dimana hasil x[n] = x.

a. Listing Program

#include <stdio.h>

#include <math.h>

#include <conio.h>

float Fungsi(float x);

float FungsiTurunan(float x);

main()

{

      int n=0;

   float x[100];

   float e = 0.0005;

   printf("           Program Newton Rapshon         \n");

   printf("           ======================         \n\n");

   printf("Persamaan Fungsi f(x) : \n");

   printf("     x*x + 3x - 10         \n\n");

   printf("x(n+1)                : \n");

   printf("     x(n)-(f(xn)/f'(xn))     \n\n");

   printf("Nilai e = 0.0005\n\n");

   printf("Masukkan nilai x Awal : "); scanf("%f",&x[0]);

   printf("==================================================================\n");

   printf("!  n  !    xn     !   f(xn)   !  f'(xn)  ! f(xn)/f'(xn) ! x(n+1) !\n");

   printf("==================================================================\n");

   do

   {

   x[n+1] = x[n] - (Fungsi(x[n])/FungsiTurunan(x[n]));

   printf("!  %d  !  %2.4f   !   %2.4f  !  %2.4f  !    %2.4f    ! %2.4f !\n", n, x[n],Fungsi(x[n]), FungsiTurunan(x[n]),Fungsi(x[n])/FungsiTurunan(x[n]),x[n+1]);

   n++;

   }while(abs(x[n-1]-x[n-2])>e);

   printf("!  %d  !  %2.4f   !   %2.4f  !  %2.4f  !    %2.4f    ! %2.4f !\n", n, x[n],Fungsi(x[n]), FungsiTurunan(x[n]),Fungsi(x[n])/FungsiTurunan(x[n]),x[n+1]);

   printf("==================================================================\n\n");

   printf("Jadi, Hasil yang memenuhi dari persamaan tersebut x = %2.4f", x[n]);

   getch();

}

float Fungsi(float x)

{

      return pow(x,2)+(3*x)-10;

}

float FungsiTurunan(float x)

{

      return 2*x+3;

}

b. Output Program

Jika x awal = 2.5

Jika x awal = -5.5

Seperti metode pembelahan, metode posisi palsu dimulai dengan dua titik a ₀ dan b ₀ sedemikian sehingga f (a ₀₎ dan f (b ₀₎ adalah tanda yang berlawanan, yang berarti dengan teorema nilai antara bahwa fungsi f memiliki akar dalam interval [a _0, b _0], dengan asumsi kontinuitas fungsi f.. Metode hasil dengan memproduksi suatu urutan menyusut interval [a _{k, k} b] yang semuanya mengandung akar dari f.

Pada k  nomor iterasi, jumlahnya:

Seperti yang dijelaskan di bawah ini, _k c adalah akar dari garis sekan melalui _(k, f _(k a)) dan (b _k, f (b _k)). . Jika f _(k a) dan f (c _k) memiliki tanda yang sama, maka kita menetapkan suatu _{k +1} = c _k dan b _{k k +1} = b, jika kita menetapkan a _{k +1} = b _k dan _{k + 1} = _k c. Proses ini diulang sampai akar adalah cukup didekati dengan baik.

Rumus di atas juga digunakan dalam metode sekan, tapi metode sekan selalu mempertahankan dua poin terakhir dihitung, sedangkan metode posisi palsu mempertahankan dua titik yang tentunya bracket akar. Di sisi lain, satu-satunya perbedaan antara metode posisi palsu dan metode pembelahan adalah bahwa yang kedua menggunakan _k c = (a _k + _k b) / 2.

Mencari akar dari garis potong.

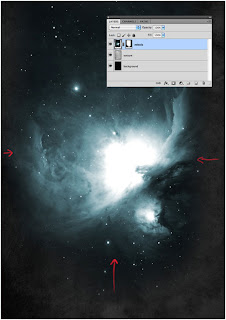
Diberikan a dan b _{k k,} kita mengkonstruksi line melalui titik _(k, f _(k a)) dan (b _k, f (b _k)), seperti yang ditunjukkan pada gambar di  atas. Perhatikan bahwa garis tersebut adalah garis potong atau akord dari grafik fungsi f. Dalam bentuk titik-lereng , hal itu dapat didefinisikan sebagai:

Kita sekarang memilih _k c menjadi akar dari garis ini, jadi c dipilih sedemikian sehingga

 Penyelesaian persamaan ini memberikan persamaan di atas untuk _k c.

Analisis.

Jika akhir titik awal a ₀ dan b ₀ dipilih sedemikian sehingga f (a ₀₎ dan f (b ₀₎ adalah tanda yang berlawanan, maka salah satu-titik akhir akan berkumpul ke akar f. Asimtotik, pada titik akhir-lain akan tetap tetap untuk semua iterasi mendatang, sementara titik akhir konvergensi menjadi diperbarui. Akibatnya, tidak seperti metode pembelahan , lebar braket tidak cenderung nol. Sebagai konsekuensinya, pendekatan linier untuk f (x), yang digunakan untuk memilih posisi palsu, tidak meningkatkan kualitas.

Salah satu contoh dari fenomena ini adalah fungsi :

f ( x ) = 2 x ³ − 4 x ² + 3 x f (x) = 2 x ³ - 4 x ² + 3 x

pada braket awal [-1,1]. Ujung kiri, -1, tidak pernah diganti dan dengan demikian lebar braket tidak pernah turun di bawah 1. Oleh karena itu, titik akhir kanan mendekati 0 pada laju linear (dengan laju konvergensi dari 2 / 3).

Meskipun kesalahpahaman untuk berpikir bahwa metode posisi palsu adalah metode yang bagus, adalah sama kesalahan untuk berpikir bahwa itu adalah unsalvageable. Modus kegagalan adalah mudah untuk mendeteksi (akhir titik-sama masih dipertahankan dua kali berturut-turut) dan mudah diatasi dengan berikutnya memilih posisi palsu dimodifikasi, seperti :

 atau

turunan-bobot salah satu titik akhir nilai untuk memaksa _k c berikutnya terjadi pada sisi fungsi. Faktor dari 2 di atas terlihat seperti hack, tetapi menjamin konvergensi superlinear (asimtotik, algoritma akan melakukan dua langkah biasa setelah setiap langkah dimodifikasi). Ada cara lain untuk memilih rescaling yang memberikan tingkat konvergensi yang lebih baik superlinear.

Penyesuaian atas, dan modifikasi sejenis lainnya untuk PERATURAN Falsi disebut Algoritma Illinois. Ford (1995) merangkum dan menganalisa varian superlinear metode modifikasi dari posisi palsu. Dilihat dari bibliografi, PERATURAN dimodifikasi metode falsi yang terkenal di tahun 1970-an dan telah kemudian lupa atau misremembered dalam buku pelajaran saat ini.

CONTOH KODE PROGRAMNYA MENGGUNAKAN C++:

# Include <stdio.h>

# Include <math.h> 

double f( double x) 

{ 

    return cos(x) - x*x*x; 

} 

FalsiMethod ganda (double s, double t, double e, int m)

{ 

    int n,side=0; 

    double r,fr,fs = f(s),ft = f(t); 

    untuk (n = 1; <n = m; n + +)

    { 

        r = (fs*t - ft*s) / (fs - ft); 

        if (fabs(ts) < e*fabs(t+s)) break ; 

        fr = f (r);

        if (fr * ft > 0) 

        { 

           t = r; ft = fr; 

           jika (sisi ==- 1) fs / = 2;

           sisi = -1;

         }

        else if (fs * fr > 0) 

        { 

          s = r; fs = fr;

          if (== sisi +1) ft / = 2;

          side = +1;

         }

        lain break;

     }

    return r; return r;

}

int main( void ) 

{ 

    printf ("% 0.15f \ n", FalsiMethod (0, 1, 5E-15, 100));

    return 0; return 0;

} 

Setelah menjalankan kode di atas, jawaban akhir adalah sekitar 0,865474033101614.

 

1. METODE BISEKSI (Bagi Dua).

•          Memanfaatkan beda tanda dua nilai batas

•          f(x_l)f(x_u) < 0 dimana l=lower (batas bawah) dan u=upper (batas atas)

•          Minimal ada satu akar

Contoh soal misalnya:  F(X) = X³ + X² – 3X - 3
Maka Penyelesainya:
 (lihat entri selanjutnya dibawah)

dan hasilnya adalah seperti gambar berikut:

Ada beberapa definisi Metode Numerik yang dikemukakan oleh ahli Matematika sebagai berikut:

•Metode Numerik: Teknik matematika yang di formulasikan untuk dapat menyeleseaikan pengoperasian aritmatika. (Chapra dan Chanale Tahun 1991)
•Metode numerik: teknik untuk merumuskan masalah matematika agar dapat diselesaikan dengan operasi hitungan yaitu: +, -, x dan / (Susila 1994; Ibraheem dan Hisyam 2003).

Jadi kesimpulannya, Metode numerik adalah suatu teknik memformulasikan masalah matematika yang diselesaikan dengan operasi aritmatika (+, -, x dan /) untuk memperoleh jawaban yang eksak. Misalnya menyelesaikan suatu persamaan.

Namun pada prinsipnya Metode numerik digunakan untuk persoalan yang penyeleseainnya berupa pendekatan dari nilai eksaknya yang menyediakan sejumlah kalkulasi aritmatika yang sulit dilakukan tanpa komputer.
Hal ini memunculkan beberapa alasan, mengapa orang menggunakan metode numerik untuk membantu memecahkan masalah, yaitu:

1.Lebih Efektif dan Efisien. Misalnya menyelesaikan persamaan tak linear, persamaan yang besar dan masalah lainnya termasuk dalam teknik dan sosial dapat diselesaikan secara analistis.

2.Tersedia dan diperdagangkan di mana saja yang dalam pengoperasiannya mencakup metode numerik.

3.Lebih leluasa dalam menggunakan metode numerik untuk memecahkan masalah yang di hadapinya.

4.Sebagai sarana untuk mengenal karakteristik komputer dan mendesain algoritma, diagram alur dan menulis program komputer sendiri.

5.Sarana untuk memperkuat kemampuan ilmu matematika.

Metode numerik juga tergolong dalam matematika terapan (applied mathematics) yang memerlukan kemahiran dalam menggunakan dan mengoperasikan komputer baik untuk paket program maupun program komputer. Paket program komputer apapun yang dikuasai dapat digunakan untuk membantu memecahkan masalah yang dihadapinya.

Keberadaan komputer dalam mata kuliah metode numerik ,yaitu yang berkaitan dengan alat dan komputasi, akar persamaan tak linear meliputi pelokasian akar, metode bagi dua, metode posisis palsu, iterasi titik tetap, metode Newton-Raphson, metode secant (talibusur); interpolasi meliputi interpolasi linear dan kuadrat, interpolasi beda terbagi Newton, interpolasi pada titik-titik berjarak sama, interpolasi largrange, interpolasi invers, dan interpolasi spline, diferensial dan integral numerik meliputi hampiran turunan, integral numerik, dan aturan komposisi, serta penggunaan metode numerik untuk memecahkan masalah sehari-hari adalah hanya sebagai alat untuk membantu dalam melakukan perhitungan numerik yang rumit dan bahkan yang sulit diselesaikan secara analistis